Complexity
What factors promote the emergence of complex evolving systems, such as life? What is “complexity” and how can it be quantified? We have approached these questions by looking for general properties of all emergent systems and by conducting computational experiments on the artificial life platform Avida (with Patrick Griffin). Our work amplifies the original studies of Szostak and coworkers, who proposed that “functional information” provides a measure of complexity in genetic polymers. The core idea is that “complexity” only has meaning in the context of “function."
These ideas are summarized in the abstract of Hazen et al. (2007): “Complex emergent systems of many interacting components, including complex biological systems, have the potential to perform quantifiable functions. Accordingly, we define “functional information,”I(Ex), as a measure of system complexity. For a given system and function, x (e.g., a folded RNA sequence that binds to GTP) and degree of function, Ex (e.g., the RNA-GTP binding energy):
I(Ex) = -log2[F(Ex)],
where F(Ex) is the fraction of all possible configurations of the system that possess a degree of function ≥Ex. Functional information, which we illustrate with letter sequences, artificial life, and biopolymers, thus represents the probability that an arbitrary configuration of a system will achieve a specific function to a specified degree. In each case we observe evidence for several distinct solutions with different maximum degrees of function – features that lead to steps in plots of information versus degree of function.
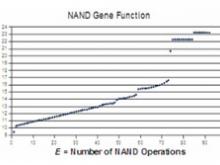
We have studied the functions of randomly-generated Avida genomes of varying lengths. In one set of computations we started with a highly functional 300-command genome and examined all possible single point mutations (300 x 25 alternate commands). We were surprised to find that the great majority of mutant genomes displayed no change in function, and a few mutant genomes had increased function.
Our tentative explanation for the discontinuities in plots of functional information versus degree of function is that for many complex systems there exist “islands of solutions” (e.g., functional Avida genomes). Here we show this phenomenon schematically as clusters of solutions projected onto an arbitrary sequence space. The different heights of relatively flat islands leads to gaps in function plots.
These ideas are closely related to studies of pattern formation, as reviewed in Hazen (2008). From the abstract: “Three principles guide natural pattern formation in both biological and nonliving systems: (1) Patterns form from interactions of numerous individual particles, or “agents,” such as sand grains, molecules, cells or organisms. (2) Assemblages of agents can adopt combinatorially large numbers of different configurations. (3) Observed patterns emerge through the selection of highly functional configurations. These three principles apply to numerous natural processes, including the origin of life and its subsequent evolution. The formalism of “functional information,” which relates the information content of a complex system to its degree of function, provides a quantitative approach to modeling the origin and evolution of patterning in living and nonliving systems.”